✨Định Lý Cuối Cùng Của Fermat
Định Lý Cuối Cùng Của Fermat
Combo 2 Cuốn Kinh Tế- Kinh Doanh Hay- Nhượng Quyền Khởi Nghiệp - Con Đường Ngắn Để Bước Ra Thế Giới+ Coach - Khởi Nghiệp Độc Lập Bằng Kỹ Năng Khai Vấn 1/ Nhượng Quyền
Tác Giả: Nhiều tác giả Ngày phát hành: 2020 Số trang: 344 Kích thước: 19 x 26 cm NXB: NXB Đại học Quốc gia Giá bìa: 268.000VND Nhật Bản là quốc gia đứng đầu về
- Vì sao Khoa Y Đại học Harvard bãi bỏ việc giảng dạy truyền thống? - Vì sao tập đoàn tài chính Goldman Sachs sa thải 598 nhân viên tài giỏi nhất? - Lý do
THỜI KỲ HẬU CORONA Diễn biến của thời cuộc là bất trắc. Trong khủng hoảng, nguy và cơ tồn tại song hành nhưng quan trọng là chúng tác động đến mọi người theo cách khác
Tập Viết Lớp 2 - Tập 2 (Theo Chương Trình Giáo Dục Phổ Thông Mới) Quyển vở này giúp em luyện viết thêm Nội dung luyện viết gắn với các yêu cầu cần đạt về
Nhật Ký Đặng Thùy Trâm (Tái Bản 2016) Một cuốn nhật kí nhặt được bên xác của một nữ Việt Cộng đã suýt bị người lính Mỹ ném vào lửa, nhưng người phiên dịch đã
Giới thiệu cuốn sách " Luật Dầu Khí 2022" do nhà xuất bản Lao Động xuất bản. Quốc hội khóa XV đã thông qua Luật Dầu khí 2022 vào ngày 14/11/2022, trong đó, quy định
Cuốn sách là những ví dụ cụ thể về các doanh nghiệp thành công trong một loạt các lĩnh vực. Khi học hỏi cách những người phụ nữ khác thành công, bạn cũng sẽ tìm
Tại sao lại có nhiều người quan tâm tới những buổi nói chuyện của chúng tôi đến vậy? Bởi vì chúng tôi đã khám phá ra ai mới thực sự là người giàu có. Và
COMBO BỘ SÁCH 151 Ý TƯỞNG CHO DOANH NGHIỆP Ảnh hưởng cá nhân của chúng ta đến từ việc ngộ rõ mình là ai, chúng ta đấu tranh cho điều gì, đâu là những ưu
Các từ đã ở trên đầu lưỡi của bạn, nhưng bạn lại không thể nhớ ra mình định nói gì. Bạn đã đến địa điểm đó hàng trăm lần, vậy tại sao bạn vẫn rẽ
Là tập hợp những cuốn sách nhằm mục đích phát triển kỹ năng nghe, hiểu, đọc, viết cho trẻ. Với cấu trúc biên soạn mang tính tương tác cao, bao gồm phần lời và câu
Sách - Trần Triều Nhàn Thoại Nhà cung cấp: Tri Thức Trẻ Books Mã hàng: 8936107812951 Nhà xuất bản: 2022 Nhà xuất bản: NXB Hội Nhà Văn Tác giả: Đồng Lạc Số trang: 268 Trọng
Bộ sách Kế hoạch bài dạy lớp 3 theo bộ sách Chân trời sáng tạo hi vọng sẽ là công cụ hữu ích để hỗ trợ giáo viên trong việc biên soạn giáo án, thiết
Hồi Ký Lý Quang Diệu ( Tập 1 ) - Câu Chuyện Singapore Câu chuyện Singapore - được bắt đầu viết từ năm 1994, và xuất bản lần đầu tiên năm 1998, kể lại những
Cuộc Chơi Khởi Nghiệp Phần 1 “Một cuốn sách cần thiết cho các chủ doanh nghiệp. Brad và Jason đã làm sáng tỏ mớ lộn xộn những hợp đồng, điều khoản của một thương vụ
Life Long Learning - Học Tập Suốt Đời - Sẵn Sàng Cho Những Công Việc Còn Chưa Ra Đời Với sự phát triển chóng mặt của công nghệ, tương lai của thị trường lao động
GIỚI THIỆU SÁCH SÁCH - tuyển tập đề kiểm tra môn ngữ văn 9 bồi dưỡng học sinh giỏi (theo cấu trúc mới) Các thầy giáo, cô giáo cùng toàn thể các em học sinh
Phiếu Bài Tập Cuối Tuần Tiếng Anh 1
Tác giả: Anneli Williams Nhà xuất bản Tổng Hợp Thành Phố Hồ Chí Minh Số trang: 144 Kích thước: 19cm x 25cm x 0.6cm Cân nặng: 250g Năm xuất bản: 2018 Công ty phát hành:
Smart Growth - 7 Bước Chuyển Mình Cho Cá Nhân Và Tổ Chức Theo nghiên cứu của tác giả, mỗi người khi học hỏi một kỹ năng mới, bắt đầu một công việc mới hoặc
1. Phía sau nghi can X “Việc nghĩ ra một bài toán vô cùng khó và việc giải bài toán đó, việc nào khó hơn?” Khi nhấn chuông cửa nhà nghi can chính của một
Bất kỳ tổ chức nào cũng đều phải đối mặt với những thay đổi lớn tới từ bên ngoài trong quá trình chyển đổi số. Vậy tổ chức của bạn phải bắt đầu từ đâu?
Combo sách giáo trình Hán ngữ MSUTONG trung cấp Giáo trình gồm 4 cuốn, mỗi cuốn 10 bài, tổng 40 bài. Mỗi bài tương ứng với một chủ điểm giao tiếp gần gũi, thiết thực.
Là một bậc thầy trong lĩnh vực tinh thần và tâm linh, Eckhart Tolle đã giúp rất nhiều người trên thế giới tìm thấy sự bình an và hạnh phúc trong cuộc sống. Cốt lõi
Những Bài Học sâu sắc Triết Lí Từ Truyện Ngôn Tình Diệp Lạc Vô Tâm: Chân Trời Góc Bể + Hãy Nhắm Mắt Khi Anh Đến 1. Chân Trời Góc Bể Bốn năm trước, quá
Từ Điển Việt – Hàn (Tái Bản 2018) Những năm gần đây người Việt học tiếng Hàn Quốc ngày càng đông do sự phát triển giao lưu mạnh mẽ giữa 2 nước Việt - Hàn.
Tác giả: Luật sư Nguyễn Ngọc Bích Ngày xuất bản: 03-2015 Kích thước: 15.5 x 23 cm Số trang: 442 GIỚI THIỆU SÁCH Nội dung quyển sách được chia làm 4 phần: Phần hai: Trình
Chỉ có một Thượng đế? Vì sao con người chịu khổ? Điều gì chờ ta sau cái chết? Hàng tỉ người trên thế giới tìm thấy ý nghĩa sống trong tôn giáo, nhưng những tư
Dòng Máu Cao Quý Bố mất khi cậu còn nhỏ tuổi, Patrick Nothomb lớn lên bên cạnh một người mẹ tư sản thường xuyên vắng mặt. Cậu được ông bà ngoại nuôi dưỡng và cưng
Combo Làm Chủ Trí Nhớ Của Bạn và Sử Dụng Trí Nhớ Của Bạn - Use Your Memory ( Tặng Kèm Bút ) Bản tặng kèm bút BTS , mẫu ngẫu nhiên và số lượng
Who? Chuyện Kể Về Danh Nhân Thế Giới: Winston Churchill Lời nói đầu/Giới thiệu sách Who? - Chuyện kể về danh nhân thế giới là bộ truyện thú vị kể về cuộc đời của các
Who? Chuyện Kể Về Danh Nhân Thế Giới - Wilhelm Roentgen Giới thiệu tác giả Lee Jongwon và Oh Youngseok: Bộ đôi sáng tạo Lee Jongwon và Oh Youngseok thường được biết đến như một
200 Miếng Bóc Dán Thông Minh - Phát Triển Chỉ Số Thông Minh IQ (2-6 Tuổi) - Tái Bản 2018 Lời nói đầu/Giới thiệu sách Đây là cuốn sách được tuyển chọn và những trò
Sách - 150 đề và bài văn hay 10 (dùng chung các bộ sgk hiện hành) TÁI BẢN LẦN 1- HA Học là một quá trình rèn luyện vất vả nhất của đời người. Điều
Kĩ Thuật Giải Nhanh Bài Toán Hay Và Khó Đại Số 10 (Biên Soạn Theo Chương Trình GDPT Mới) Các em học sinh lớp 10 thân mến! Vậy là các em đã bước vào đầu
"Con đang đọc chuyện cho Owly, sau đó thì Gà Con tới, rồi anh chị em và họ hàng của cậu ấy cũng tới, và cuối cùng là tất cả các bạn đều đến, họ
Sách - 23 Chuyên Đề Giải 1001 Bài Toán Sơ Cấp - Dành Cho Học Sinh Lớp 9 Cuốn sách gồm các chuyên đề sau : Chuyên đề 1. Biền đổi đồng nhất Chuyên đề
7 Loại Hình Thông Minh Nội dung cuốn sách "7 loại hình thông minh" gồm có: - Những hiểu biết căn bản làm nền tảng về quá trình diễn ra hoạt động nhận thức của
Bộ Truyện Cổ Việt Nam Song Ngữ Việt – Anh (5 Cuốn) “Nếu bạn muốn con thông minh, hãy đọc truyện cổ tích cho chúng. Nếu bạn muốn con mình thông minh hơn nữa, hãy
Công ty phát hành: Wabooks Nhà xuất bản: NXB Thanh Niên Tác giả: Fuku Mitsu Loại bìa: Bìa mềm Số trang: 28 trang Mực in thành phần dầu hạt lanh, không chứa chì và thủy
Tác giả: Ths. Trần Thị Thu Hà , Gs. Jane Fisher , cùng cộng sự Nhà xuất bản: Thế giới Số trang: 192 Kích thước: 14.5 x 20.5cm Ngày phát hành: 12-2022 Bạn có cảm
Trong phút bốc đồng, cô nhân viên hiệu sách Michiru bỏ lại công việc, bạn trai và gia đình, rời khỏi miền quê ven biển bình lặng để chạy theo một người đàn ông có
SÁCH - hướng dẫn giải bài tập toán 2 tập 2 bám sát sgk chân trời sáng tạo Cuốn sách Hướng dẫn giải bài tập Toán 2 - Tập 2 được biên soạn nhằm trợ
101 Bước Vẽ Chì Căn Bản Trong Hội Họa Nhà xuất bản : Nhà Xuất Bản Thanh Hóa. Công ty phát hành : Văn Lang. Tác giả : Robert Capitolo. Kích thước : 19 x
Từ ngàn xưa, người phương Đông luôn quan niệm rằng: Người lãnh đạo nhất thiết phải hội tụ “ thuật lãnh đạo, thuật quản trị, thuật dụng ngôn và thuật xử thế” thì mới thu
Hành Trình Theo Chân Bác Cuốn sách Hành Trình Theo Chân Bác được biên soạn dựa trên lời bình 2 bộ phim: Ký sự Hành trình theo chân Bác và Hồ Chí Minh - Một
Nguồn Gốc - Nỗi Hoài Niệm Về Những Thuở Ban Đầu Cuốn sách này nhằm mở ra cho độc giả những cánh cửa của thế giới vô cùng lớn - các thiên hà xa xôi,
"Không giống như các chế độ khác trên khắp thế giới đã từng có những quyết tâm tương tự nhưng cuối cùng vẫn sụp đổ, các nhà lãnh đạo Trung Quốc cho đến nay vẫn
 Sách - Phiếu Bài Tập Cuối Tuấn Môn Tiếng Việt Lớp 3 - Biên Soạn Theo Chương Trình GDPT Mới - Hồng Ân
Sách - Phiếu Bài Tập Cuối Tuấn Môn Tiếng Việt Lớp 3 - Biên Soạn Theo Chương Trình GDPT Mới - Hồng Ân Phiếu Bài Tập Cuối Tuấn Môn Tiếng Việt Lớp 3 (Biên Soạn Theo Chương Trình GDPT Mới) Được biên soạn bám sát chương trình Giáo dục Tiểu học, theo Chương trình mới của Bộ Giáo
Kho tàng truyện cổ tích Việt Nam vô cùng phong phú và đa dạng, đã được giới thiệu tới bạn đọc thông qua nhiều tuyển tập khác nhau. Nhằm giới thiệu đến bạn đọc những
Em Luyện Viết Tiếng Anh Và Nhớ Từ Vựng Smart Star 2 “EM LUYỆN VIẾT TIẾNG ANH VÀ NHỚ TỪ VỰNG” được biên soạn nhằm giúp các em bước đầu làm quen với các từ
Hương Hoa Tình Yêu Jom là kiến trúc sư phụ trách trùng tu căn nhà cổ nằm cạnh sông Ping, tại tỉnh Chiang Mai đầy sương mù. Cảnh vật nơi đây khiến cậu có cảm
THAY ĐỔI CUỘC CHƠI TRONG KINH DOANH Kể từ sau cuộc khủng hoảng tài chính toàn cầu năm 2008, các doanh nghiệp đã phải thay đổi toàn diện để trụ vững trên thị trường. Những
Kính Vạn Hoa (Phiên Bản 18 Tập) - Tập 16 Bộ ấn phẩm Kính Vạn Hoa phiên bản mới 18 tập, minh họa của họa sĩ Đỗ Hoàng Tường. Nhận định "Nguyễn Nhật Ánh được
Giới thiệu sách: Cờ vua - những bài học đầu tiên là tập sách mở màn cho 1 bộ gồm 9 cuốn sách mà tác giả tham vọng có thể xem chúng như "chương trình
You Can Win - Bí Quyết Của Người Chiến Thắng Với cách đặt vấn đề dễ hiểu, thiết thực và sâu sắc, Bí quyết của người chiến thắng sẽ giúp bạn tránh rơi vào cảm
Sách - Kĩ Năng Giải Toán Căn Bản Và Mở Rộng Lớp 9 - Dùng Chung Cho Các Bộ SGK Hiện Hành Cuốn sách Kĩ năng giải toán căn bản và mở rộng 9 này
Phúc Ông Tự Truyện Cuốn tự truyện kể về những bước thăng trầm của cuộc đời Fukuzawa Yukichi từ khi sinh ra cho đến những năm tháng tuổi già. Qua từng chi tiết nhỏ, từng
Sự Thật chính là Sự Vui” của nhà thơ Như Huy Chào bạn, ta gặp lại nhau. Hôm nay, tôi mời bạn đọc tập thơ “Sự Thật chính là Sự Vui” của nhà thơ Như
👁️ 8 | ⌚2025-09-12 23:41:21.153
VNĐ: 126,000
Mua hàng tại Shopee giảm thêm 30%



VNĐ: 126,000
Mua hàng tại Shopee giảm thêm 30%



Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý
Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý cuối cùng của Fermat. Nó nổi tiếng vì dạng của nó quá đơn giản.
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat “xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat - Hành Trình Đi Tìm Lời Giải Cho Bài Toán Khó Bậc Nhất Trong Lịch Sử “xn + yn = zn, trong đó n
Định Lý Cuối Cùng Của Fermat
“xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng do lề quá hẹp không thể
“xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng do lề quá hẹp không thể
Giới thiệu tóm tắt tác phẩm: “xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng
Được xem là quyển sách viết về toán học dành cho đại chúng đầu tiên trở thành best - seller " Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này,
Combo Sách Kiến Thức Bách Khoa Hay : Những Câu Hỏi Lớn Vật Lý + Những Câu Hỏi Lớn Toán Học ( Tặng Kèm Postcard HAPPY LIFE ) Hai cuốn sách Những Câu Hỏi Lớn
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Những Câu Hỏi Lớn đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Bộ 2 cuốn sách tìm hiểu về lịch sử toán học: Toán Học Một Thiên Tiểu Thuyết - Những Câu Hỏi Lớn Toán Học - Toán Học Một Thiên Tiểu Thuyết Hầu hết mọi người
Những Câu Hỏi Lớn - Toán Học NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Bản ĐB (Bìa cứng - Chữ kí của tác giả: GS.Ngô Bảo Châu) - Tác giả: GS. Ngô Bảo
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Tác giả: GS. Ngô Bảo Châu - TS. Đỗ Việt Cường - Nhà xuất bản Đại học Quốc gia Hà
Lý thuyết số, từ nhiều góc độ, được xem là điểm khởi đầu của toán học. Không chỉ là nơi khơi nguồn cho nhiều nhánh toán học phát triển, mà nó còn đem đến những
Cuối năm 2017, chúng ta chứng kiến sự nổi lên của D. ouyin, một ứng dụng đến từ T. rung Q. uốc, và sự ảnh hưởng của nó đến những người xung quanh. Mọi người
Tôi muốn viết một cuốn sách hướng dẫn cho người mới bắt đầu về cách làm việc này: cuốn sách dành cho những ai ghét tự quảng cáo bản thân. Có thể gọi đây là
BA ĐƯỜNG LUÂN HỒI - TRỌN BỘ 4 QUYỂN VỀ TÁC GIẢ: Vĩ Ngư là tác giả nổi tiếng của trang văn học mạng Tấn Giang chuyên viết về thể loại phiêu lưu linh dị
Thảm Nhựa Lót Cốp Sau Ô Tô + Chất liệu nhựa dẻo. Không mùi hôi không thấm nước, độ dày khoảng 6mm. + Bộ bao gồm 1 miếng, cho nền cốp rất vừa vặn và
Máy ép chậm trái cây ELMICH EDA-0860, Hàng chính hãng, Ống ép được quả lớn, Xay ép êm ái - JoyMall THÔNG TIN SẢN PHẨM Công suất 220W Tốc độ ép 55 vòng/phút Dung tích
Tên tác phẩm Anh trai nhân vật chính – Tập 1 Tác giả Tiên Sắc Xám Thể loại Tiểu thuyết hư cấu Thương hiệu Ganesh Books Nhà xuất bản NXB Thanh Niên Năm xuất bản
SÁCH - Chuyển đổi toàn diện mô hình kinh doanh Tác giả Alexander Zimmermann , Carsten Linz , Günter Müller-Stewens ---- CHUYỂN ĐỔI TOÀN DIỆN MÔ HÌNH KINH DOANH Tạo lợi thế cạnh tranh trong
ƯU ĐIỂM CUỐN SÁCH KĨ NĂNG BIÊN DỊCH - PHIÊN DỊCH TIẾNG TRUNG ỨNG DỤNG - Cuốn sách cung cấp từ vựng, hình ảnh minh họa, ghi chú nhanh những kiến thức cơ bản và
Since its original publication by Little, Brown and Company in 1942, Edith Hamilton's Mythology has sold millions of copies throughout the world and established itself as a perennial bestseller in its various available formats: hardcover,
Tết Quý Mão 2023 cả nước ta kỷ niệm một ngày lễ lớn: 55 năm cuộc Tổng Tiến công và nổi dậy Xuân Mậu Thân 1968. Câu lạc bộ Truyền thống Thành Đoàn cùng Ban
Captain Underpants #5: Captain Underpants and the Wrath of the Wicked Wedgie Woman (Colour Edition) Captain Underpants is back for a bad hair day gone wild - this time in full colour! With more than
Chinh phục không gian có lẽ là cuộc chinh phục kì diệu và vĩ đại nhất mà con người đã và đang thực hiện. Khám phá vũ trụ bao la là ước mơ từ hàng
Anna - Nếu một người trở về từ tương lai, cô ta sẽ làm xáo trộn thực tại của thế giới ------------ ANNA được sinh ra trên một hành tinh của những người thuận tay
Bốn Mùa, Trời Và Đất Bốn mùa (1938), Trời và Đất (1942), mượn ẩn dụ từ sự trải nghiệm cuộc sống, qua những quy luật linh thiêng mà hiển nhiên: đất- trời, cao- thấp, sự
3000 Tests Elementary To Intermediate Devised an easy self - checking guide, this book serves as a valuable tool that helps students in reviewing their knowledge of grammar and vocabulary of each language level they
ヴィンランド・サガ - Vinland Saga 23 - fahasa
Bé chuẩn bị vào lớp 1! Làm sao để chuẩn bị cho bé thật tốt? Làm thế nào để bé không bỡ ngỡ khi bước vào một giai đoạn hoàn toàn mới này? Bộ sách
Vở Tập Viết Có Mẫu Chữ - Quyển 2 Trước khi vào lớp 1, các bé cần phải được làm quen với các chữ viết cơ bản, để giúp bé không bỡ ngỡ khi mới
Giáo sư Đặng Hùng Võ và những người bạn nhà báo Trong kỷ nguyên thông tin, báo chí giúp cho mỗi ý tưởng tốt đi tới dân nhanh nhất! I. AI NÊN ĐỌC CUỐN SÁCH
Aquarium Snap Children can learn about turn-taking, rules and winning and losing while enjoying vibrant illustrations of sea creatures, from jellyfish, rays and clownfish to seahorses, sharks and starfish.
**Chứng minh của Wiles về định lý cuối cùng của Fermat** là chứng minh toán học của nhà toán học người Anh Andrew Wiles về một trường hợp đặc biệt của định lý Module đối
Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý
Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý
Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý cuối cùng của Fermat. Nó nổi tiếng vì dạng của nó quá đơn giản.
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat “xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat - Hành Trình Đi Tìm Lời Giải Cho Bài Toán Khó Bậc Nhất Trong Lịch Sử “xn + yn = zn, trong đó n
Định Lý Cuối Cùng Của Fermat
phải|Bài toán II.8 trong _Arithmetica_ của Diophantus, với chú giải của Fermat và sau đó trở thành định lý Fermat cuối cùng (ấn bản 1670) **Định lý cuối cùng của Fermat** (hay còn gọi là
“xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng do lề quá hẹp không thể
phải|nhỏ|389x389px|[[Định lý Pythagoras|Định lý Pitago có ít nhất 370 cách chứng minh đã biết ]] Trong toán học và logic, một **định lý** là một mệnh đề phi hiển nhiên đã được chứng minh là
“xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng do lề quá hẹp không thể
Giới thiệu tóm tắt tác phẩm: “xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng
Được xem là quyển sách viết về toán học dành cho đại chúng đầu tiên trở thành best - seller " Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này,
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Những Câu Hỏi Lớn - Toán Học NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại
**Định lý của Ribet** (hay **Phỏng đoán Epsilon - Phỏng đoán ε**, tiếng Anh: **Ribet's theorem**) là một phần của lý thuyết số. Nó đề cập tới đến các thuộc tính của các biểu diễn
**Pierre de Fermat** (, phiên âm: _"Pi-e Đờ Phéc-ma"_, 17 tháng 8 năm 1607 ## Công việc Công trình tiên phong của Fermat trong Hình học giải tích (_Methodus ad disquirendam maximam et minimam et
**Lý thuyết số đại số** là một nhánh của lý thuyết số sử dụng các kỹ thuật của đại số trừu tượng để nghiên cứu các số nguyên, các số hữu tỷ và các tổng
Combo Sách Kiến Thức Bách Khoa Hay : Những Câu Hỏi Lớn Vật Lý + Những Câu Hỏi Lớn Toán Học ( Tặng Kèm Postcard HAPPY LIFE ) Hai cuốn sách Những Câu Hỏi Lớn
nhỏ|Các bảng số học dành cho trẻ em, Lausanne, 1835 **Số học** là phân nhánh toán học lâu đời nhất và sơ cấp nhất, được hầu hết mọi người thường xuyên sử dụng từ những
thumb|right|Các thao tác bước xoay [[Rubik|khối lập phương Rubik tạo thành nhóm khối lập phương Rubik.]] Trong toán học, một **nhóm** (group) là một tập hợp các phần tử được trang bị một phép toán
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Những Câu Hỏi Lớn đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
**Người tiếp xúc UFO** (tiếng Anh: _Contactees_) là những người tuyên bố đã từng tiếp xúc với người ngoài hành tinh. Một số chủ thể kể lại có những cuộc gặp gỡ đang diễn ra,
**Thomas Andrew "Tom" Lehrer** (9 tháng 4 năm 1928 - 26 tháng 7 năm 2025) là một nhạc sĩ-ca sĩ, nghệ sĩ piano, nhà trào phúng và nhà toán học, nửa sau sự nghiệp chuyển
nhỏ|Biểu tượng **vô tận** **Vô hạn, vô cực, vô tận** (ký hiệu: ∞) là một khái niệm mô tả một cái gì đó mà không có bất kỳ giới hạn nào, hoặc một cái gì
Trong lý thuyết số, số nguyên tố được gọi là **số nguyên tố Sophie Germain** nếu cũng là số nguyên tố. Số của số nguyên tố
thumb| với giá trị . Trong số học, **lập phương** của một số _n_ có nghĩa là nhân 3 lần giá trị của nó với nhau: :. Hay cũng có thể hiểu là lấy tích
**Hằng số Gelfond–Schneider** hay **số Hilbert** là hai mũ căn bậc hai của hai: :2 = ... và được chứng minh là số siêu việt bởi Rodion Kuzmin năm 1930. Năm 1934, Aleksandr Gelfond và
Bộ 2 cuốn sách tìm hiểu về lịch sử toán học: Toán Học Một Thiên Tiểu Thuyết - Những Câu Hỏi Lớn Toán Học - Toán Học Một Thiên Tiểu Thuyết Hầu hết mọi người
Những Câu Hỏi Lớn - Toán Học NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
thumb|[[Đồ thị nửa lôgarit của các nghiệm của phương trình cho số nguyên , , và , với . Dải màu xanh lá cây đánh dấu các giá trị được chứng
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Bản ĐB (Bìa cứng - Chữ kí của tác giả: GS.Ngô Bảo Châu) - Tác giả: GS. Ngô Bảo
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Tác giả: GS. Ngô Bảo Châu - TS. Đỗ Việt Cường - Nhà xuất bản Đại học Quốc gia Hà
Lý thuyết số, từ nhiều góc độ, được xem là điểm khởi đầu của toán học. Không chỉ là nơi khơi nguồn cho nhiều nhánh toán học phát triển, mà nó còn đem đến những
thế=Groups of two to twelve dots, showing that the composite numbers of dots (4, 6, 8, 9, 10, and 12) can be arranged into rectangles but the prime numbers cannot|nhỏ| Hợp số có thể được
**Leonhard Euler** ( , ; 15 tháng 4 năm 170718 tháng 9 năm 1783) là một nhà toán học, nhà vật lý học, nhà thiên văn học, nhà lý luận và kỹ sư người Thụy
**Johann Carl Friedrich Gauß** (; ; ; 30 tháng 4 năm 1777 – 23 tháng 2 năm 1855) là một nhà toán học và nhà khoa học người Đức tài năng, người đã có nhiều
**Blaise Pascal** (; 19 tháng 6 năm 1623 – 19 tháng 8 năm 1662) là nhà toán học, vật lý, nhà phát minh, tác gia, và triết gia Công giáo người Pháp. Là cậu bé
 Combo 2 Cuốn Kinh Tế- Kinh Doanh Hay- Nhượng Quyền Khởi Nghiệp - Con Đường Ngắn Để Bước Ra Thế Giới+ Coach - Khởi Nghiệp Độc Lập Bằng Kỹ Năng Khai Vấn
Combo 2 Cuốn Kinh Tế- Kinh Doanh Hay- Nhượng Quyền Khởi Nghiệp - Con Đường Ngắn Để Bước Ra Thế Giới+ Coach - Khởi Nghiệp Độc Lập Bằng Kỹ Năng Khai Vấn  Sách - Giao tiếp tiếng Nhật trong kinh doanh Basic 2 - First News
Sách - Giao tiếp tiếng Nhật trong kinh doanh Basic 2 - First News  EIGHT - 8 Cách Làm Chủ Trí Thông Minh Nhân Tạo
EIGHT - 8 Cách Làm Chủ Trí Thông Minh Nhân Tạo  Thời Kỳ Hậu Corona: Luôn Có Cơ Hội Trong Khủng Hoảng
Thời Kỳ Hậu Corona: Luôn Có Cơ Hội Trong Khủng Hoảng  Sách - Tập Viết Lớp 2 - Tập 2 - Theo Chương Trình Giáo Dục Phổ Thông Mới - Hồng Ân
Sách - Tập Viết Lớp 2 - Tập 2 - Theo Chương Trình Giáo Dục Phổ Thông Mới - Hồng Ân  Nhật Ký Đặng Thùy Trâm (Tái Bản)
Nhật Ký Đặng Thùy Trâm (Tái Bản)  Luật Dầu khí 2022
Luật Dầu khí 2022  Mẹ Bỉm Sữa Kinh Doanh Online - Từ Lên Ý Tưởng Đến Tạo Thu Nhập Chỉ Trong 12 Tuần
Mẹ Bỉm Sữa Kinh Doanh Online - Từ Lên Ý Tưởng Đến Tạo Thu Nhập Chỉ Trong 12 Tuần  Sách Bẻ Khóa Bí Mật Triệu Phú (Tái Bản)
Sách Bẻ Khóa Bí Mật Triệu Phú (Tái Bản)  Trí Nhớ Minh Mẫn, Tư Duy Sắc Sảo: Các Chiến Lược Chống Lão Hóa Cho Bộ Não Của Bạn
Trí Nhớ Minh Mẫn, Tư Duy Sắc Sảo: Các Chiến Lược Chống Lão Hóa Cho Bộ Não Của Bạn  Truyện Cổ Tích Việt Nam Đặc Sắc - Sự Tích Dưa Hấu
Truyện Cổ Tích Việt Nam Đặc Sắc - Sự Tích Dưa Hấu  Trần Triều Nhàn Thoại ( Đồng Lạc )
Trần Triều Nhàn Thoại ( Đồng Lạc )  Sách - Kế hoạch bài dạy môn Toán lớp 3 (bộ Chân trời sáng tạo)
Sách - Kế hoạch bài dạy môn Toán lớp 3 (bộ Chân trời sáng tạo)  Trạm Đọc Official | Hồi Ký Lý Quang Diệu ( Tập 1 ) - Câu Chuyện Singapore
Trạm Đọc Official | Hồi Ký Lý Quang Diệu ( Tập 1 ) - Câu Chuyện Singapore  Sách - Life Long Learning - Học Tập Suốt Đời - Sẵn Sàng Cho Những Công Việc Còn Chưa Ra Đời
Sách - Life Long Learning - Học Tập Suốt Đời - Sẵn Sàng Cho Những Công Việc Còn Chưa Ra Đời  Sách - Tuyển Tập Đề Kiểm Tra Môn Ngữ Văn Lớp 9 - Bồi Dưỡng Học Sinh Giỏi - Hồng Ân
Sách - Tuyển Tập Đề Kiểm Tra Môn Ngữ Văn Lớp 9 - Bồi Dưỡng Học Sinh Giỏi - Hồng Ân 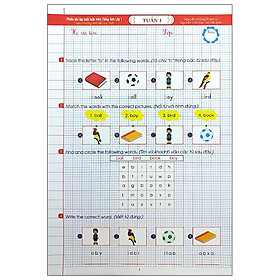 Phiếu Bài Tập Cuối Tuần Tiếng Anh 1
Phiếu Bài Tập Cuối Tuần Tiếng Anh 1  Sách - Trọn Bộ 6 Cuốn Collins English For Exams: Writing, Reading, Speaking, Listening, Grammar, Vocabularry - Nhân Trí Việt
Sách - Trọn Bộ 6 Cuốn Collins English For Exams: Writing, Reading, Speaking, Listening, Grammar, Vocabularry - Nhân Trí Việt  Sách - Smart Growth - 7 Bước Chuyển Mình Cho Cá Nhân Và Tổ Chức
Sách - Smart Growth - 7 Bước Chuyển Mình Cho Cá Nhân Và Tổ Chức  Combo 2 cuốn sách: Phía sau nghi can X + Ring - Vòng tròn ác nghiệt
Combo 2 cuốn sách: Phía sau nghi can X + Ring - Vòng tròn ác nghiệt  Sách: Digital Transformation - Chuyển đổi số - 5 giai đoạn triển khai công nghệ số cho doanh nghiệp
Sách: Digital Transformation - Chuyển đổi số - 5 giai đoạn triển khai công nghệ số cho doanh nghiệp  Combo sách giáo trình Hán ngữ MSUTONG trung cấp
Combo sách giáo trình Hán ngữ MSUTONG trung cấp  Sách - Trọn Bộ Sách Tác Giả Eckhart Tolle (5 Cuốn)
Sách - Trọn Bộ Sách Tác Giả Eckhart Tolle (5 Cuốn)  Những Bài Học sâu sắc Triết Lí Từ Truyện Ngôn Tình Diệp Lạc Vô Tâm: Chân Trời Góc Bể + Hãy Nhắm Mắt Khi Anh Đến ( Tập 2)
Những Bài Học sâu sắc Triết Lí Từ Truyện Ngôn Tình Diệp Lạc Vô Tâm: Chân Trời Góc Bể + Hãy Nhắm Mắt Khi Anh Đến ( Tập 2)  Từ Điển Việt – Hàn (Tái Bản 2018)
Từ Điển Việt – Hàn (Tái Bản 2018)  Sách Tư Duy Pháp Lý Của Luật Sư- Nhìn Thật Rộng Và Đánh Tập Trung
Sách Tư Duy Pháp Lý Của Luật Sư- Nhìn Thật Rộng Và Đánh Tập Trung  Tôn Giáo - Khái Lược Những Tư Tưởng Lớn
Tôn Giáo - Khái Lược Những Tư Tưởng Lớn  Dòng Máu Cao Quý
Dòng Máu Cao Quý  Combo Làm Chủ Trí Nhớ Của Bạn và Sử Dụng Trí Nhớ Của Bạn - Use Your Memory ( Tặng Kèm Bút )
Combo Làm Chủ Trí Nhớ Của Bạn và Sử Dụng Trí Nhớ Của Bạn - Use Your Memory ( Tặng Kèm Bút )  Who? Chuyện Kể Về Danh Nhân Thế Giới: Winston Churchill
Who? Chuyện Kể Về Danh Nhân Thế Giới: Winston Churchill  Who? Chuyện Kể Về Danh Nhân Thế Giới - Wilhelm Roentgen
Who? Chuyện Kể Về Danh Nhân Thế Giới - Wilhelm Roentgen  200 Miếng Bóc Dán Thông Minh - Phát Triển Chỉ Số Thông Minh IQ (2-6 Tuổi) - Tái Bản 2018
200 Miếng Bóc Dán Thông Minh - Phát Triển Chỉ Số Thông Minh IQ (2-6 Tuổi) - Tái Bản 2018  Sách - 150 Đề Và Bài Văn Hay Lớp 10 - Dùng Chung Các Bộ SGK Hiện Hành - Hồng Ân
Sách - 150 Đề Và Bài Văn Hay Lớp 10 - Dùng Chung Các Bộ SGK Hiện Hành - Hồng Ân  Sách - Kĩ Thuật Giải Nhanh Bài Toán Hay Và Khó Đại Số Lớp 10 - Dùng Chung Các Bộ SGK Hiện Hành - Hồng Ân
Sách - Kĩ Thuật Giải Nhanh Bài Toán Hay Và Khó Đại Số Lớp 10 - Dùng Chung Các Bộ SGK Hiện Hành - Hồng Ân  Cú nhỏ - Tớ sẽ không đọc
Cú nhỏ - Tớ sẽ không đọc  Sách - 23 Chuyên Đề Giải 1001 Bài Toán Sơ Cấp - Dành Cho Học Sinh Lớp 9 - Hồng Ân
Sách - 23 Chuyên Đề Giải 1001 Bài Toán Sơ Cấp - Dành Cho Học Sinh Lớp 9 - Hồng Ân  7 Loại Hình Thông Minh (Tặng kèm sổ tay)
7 Loại Hình Thông Minh (Tặng kèm sổ tay)  Bộ Truyện Cổ Việt Nam Song Ngữ Việt – Anh (5 Cuốn)
Bộ Truyện Cổ Việt Nam Song Ngữ Việt – Anh (5 Cuốn)  Sách Ehon - Leng Keng - Dành cho trẻ từ 0 - 6 tuổi
Sách Ehon - Leng Keng - Dành cho trẻ từ 0 - 6 tuổi  Sách - Nuôi con không áp lực - Cuốn 2: Cùng con bước vào đời (Bé 0-1 tuổi) - Nhã Nam Official
Sách - Nuôi con không áp lực - Cuốn 2: Cùng con bước vào đời (Bé 0-1 tuổi) - Nhã Nam Official  Một Chuyện Đời
Một Chuyện Đời  Sách - Hướng Dẫn Giải Bài Tập Toán Lớp 2 - Tập 2 - Bám Sát SGK Chân Trời Sáng Tạo - Hồng Ân
Sách - Hướng Dẫn Giải Bài Tập Toán Lớp 2 - Tập 2 - Bám Sát SGK Chân Trời Sáng Tạo - Hồng Ân  101 Bước Vẽ Chì Căn Bản Trong Hội Họa
101 Bước Vẽ Chì Căn Bản Trong Hội Họa  Combo 4 sách Tứ thư lãnh đạo: Thuật lãnh đạo + Thuật quản trị + Thuật xử thế + Thuật dụng ngôn
Combo 4 sách Tứ thư lãnh đạo: Thuật lãnh đạo + Thuật quản trị + Thuật xử thế + Thuật dụng ngôn  Hành Trình Theo Chân Bác
Hành Trình Theo Chân Bác  Nguồn Gốc - Nỗi Hoài Niệm Về Những Thuở Ban Đầu
Nguồn Gốc - Nỗi Hoài Niệm Về Những Thuở Ban Đầu  BÀN VỀ TRUNG QUỐC: Tiết lộ của người trong cuộc về siêu cường kinh tế mới - HENRY M. PAULSON, JR - Nxb Chính trị quốc gia Sự Thật – bìa mềm
BÀN VỀ TRUNG QUỐC: Tiết lộ của người trong cuộc về siêu cường kinh tế mới - HENRY M. PAULSON, JR - Nxb Chính trị quốc gia Sự Thật – bìa mềm  Sách - Truyện xưa nước Nam - tập 2 - Truyện các tiên thánh, tổ nghề và nhân vật lịch sử (bìa cứng)
Sách - Truyện xưa nước Nam - tập 2 - Truyện các tiên thánh, tổ nghề và nhân vật lịch sử (bìa cứng)  Sách - Em Luyện Viết Tiếng Anh Và Nhớ Từ Vựng Smart Star Lớp 2 - Bám Sát SGK I-Learn Smart Start 2 - Hồng Ân
Sách - Em Luyện Viết Tiếng Anh Và Nhớ Từ Vựng Smart Star Lớp 2 - Bám Sát SGK I-Learn Smart Start 2 - Hồng Ân  Hương Hoa Tình Yêu - Tập 1
Hương Hoa Tình Yêu - Tập 1  Thay Đổi Cuộc Chơi Trong Kinh Doanh
Thay Đổi Cuộc Chơi Trong Kinh Doanh  Kính Vạn Hoa (Phiên Bản 18 Tập) - Tập 16
Kính Vạn Hoa (Phiên Bản 18 Tập) - Tập 16  Sách - Cờ Vua tập 2 : Ván Cờ Hoàn Hảo
Sách - Cờ Vua tập 2 : Ván Cờ Hoàn Hảo  You Can Win - Bí Quyết Của Người Chiến Thắng (Tái Bản)
You Can Win - Bí Quyết Của Người Chiến Thắng (Tái Bản)  Sách - Kĩ Năng Giải Toán Căn Bản Và Mở Rộng Lớp 9 - Dùng Chung Cho Các Bộ SGK Hiện Hành - Hồng Ân
Sách - Kĩ Năng Giải Toán Căn Bản Và Mở Rộng Lớp 9 - Dùng Chung Cho Các Bộ SGK Hiện Hành - Hồng Ân  Phúc Ông Tự Truyện
Phúc Ông Tự Truyện  Sự Thật Chính Là Sự Vui - Như Huy
Sự Thật Chính Là Sự Vui - Như Huy  Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh
Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh  Định Lý Cuối Cùng Của Fermat
Định Lý Cuối Cùng Của Fermat  Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat  Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat - Hành Trình Đi Tìm Lời Giải Cho Bài Toán Khó Bậc Nhất Trong Lịch Sử (Tái Bản 2023)
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat - Hành Trình Đi Tìm Lời Giải Cho Bài Toán Khó Bậc Nhất Trong Lịch Sử (Tái Bản 2023)  (In lần thứ 8 năm 2023 – Tủ sách Khoa học khám phá) - ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT - Simon Singh – Phạm Văn Thiều, Phạm Việt Hưng dịch - Nhà xuất bản Trẻ
(In lần thứ 8 năm 2023 – Tủ sách Khoa học khám phá) - ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT - Simon Singh – Phạm Văn Thiều, Phạm Việt Hưng dịch - Nhà xuất bản Trẻ  ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT
ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT  ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT - Simon Singh - Phạm Văn Thiều, Phạm Việt Hưng dịch - (bìa mềm)
ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT - Simon Singh - Phạm Văn Thiều, Phạm Việt Hưng dịch - (bìa mềm)  Sách - Định Lý Cuối Cùng Của Fermat - NXB Trẻ
Sách - Định Lý Cuối Cùng Của Fermat - NXB Trẻ  Combo Sách Kiến Thức Bách Khoa Hay : Những Câu Hỏi Lớn Vật Lý + Những Câu Hỏi Lớn Toán Học ( Tặng Kèm Postcard HAPPY LIFE )
Combo Sách Kiến Thức Bách Khoa Hay : Những Câu Hỏi Lớn Vật Lý + Những Câu Hỏi Lớn Toán Học ( Tặng Kèm Postcard HAPPY LIFE )  Những Câu Hỏi Lớn - Toán Học
Những Câu Hỏi Lớn - Toán Học  Những Câu Hỏi Lớn Toán Học ( Tái bản)
Những Câu Hỏi Lớn Toán Học ( Tái bản)  Những Câu Hỏi Lớn Toán Học
Những Câu Hỏi Lớn Toán Học  Những Câu Hỏi Lớn Toán Học (Tái Bản)
Những Câu Hỏi Lớn Toán Học (Tái Bản)  Bộ 2 cuốn sách tìm hiểu về lịch sử toán học: Toán Học Một Thiên Tiểu Thuyết - Những Câu Hỏi Lớn Toán Học
Bộ 2 cuốn sách tìm hiểu về lịch sử toán học: Toán Học Một Thiên Tiểu Thuyết - Những Câu Hỏi Lớn Toán Học  Sách - Những câu hỏi lớn – Toán học
Sách - Những câu hỏi lớn – Toán học  Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Bản ĐB (Bìa cứng - Chữ kí của tác giả: GS.Ngô Bảo Châu)
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Bản ĐB (Bìa cứng - Chữ kí của tác giả: GS.Ngô Bảo Châu)  Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số  LÝ THUYẾT SỐ SƠ CẤP - Phương Pháp Sơ Cấp Trong Lý Thuyết Số - Ngô Bảo Châu, Đỗ Việt Cường - NXB Đại Học Quốc Gia Hà Nội
LÝ THUYẾT SỐ SƠ CẤP - Phương Pháp Sơ Cấp Trong Lý Thuyết Số - Ngô Bảo Châu, Đỗ Việt Cường - NXB Đại Học Quốc Gia Hà Nội  T. IKTOK KHUYNH ĐẢO THẾ GIỚI NHƯ THẾ NÀO? – Matthew Brennan - Vân Anh và Ngọc Diệu dịch – SAIGON Books – NXB Thế Giới (Bìa mềm)
T. IKTOK KHUYNH ĐẢO THẾ GIỚI NHƯ THẾ NÀO? – Matthew Brennan - Vân Anh và Ngọc Diệu dịch – SAIGON Books – NXB Thế Giới (Bìa mềm)  Nghệ Thuật PR Bản Thân (Tặng Kèm Bookmark Tiki)
Nghệ Thuật PR Bản Thân (Tặng Kèm Bookmark Tiki)  Sách Tiểu Thuyết - Ba Đường Luân Hồi - Vĩ Ngư (trọn bộ 4 tập) - Phúc Minh Books
Sách Tiểu Thuyết - Ba Đường Luân Hồi - Vĩ Ngư (trọn bộ 4 tập) - Phúc Minh Books  Thảm Nhựa Lót Cốp Sau Dành Cho Xe Ô Tô Kia Rio 2017
Thảm Nhựa Lót Cốp Sau Dành Cho Xe Ô Tô Kia Rio 2017  Máy ép chậm trái cây ELMICH EDA-0860, Hàng chính hãng, Ống ép được quả lớn, Xay ép êm ái - JoyMall
Máy ép chậm trái cây ELMICH EDA-0860, Hàng chính hãng, Ống ép được quả lớn, Xay ép êm ái - JoyMall  Sách Anh Trai Nhân Vật Chính – Tập 1 - Tiên Sắc Xám
Sách Anh Trai Nhân Vật Chính – Tập 1 - Tiên Sắc Xám  Chuyển đổi toàn diện mô hình kinh doanh - Bản Quyền
Chuyển đổi toàn diện mô hình kinh doanh - Bản Quyền  Sách - Thực Hành Biên Dịch Phiên Dịch Tiếng Trung Ứng Dụng - Megabook
Sách - Thực Hành Biên Dịch Phiên Dịch Tiếng Trung Ứng Dụng - Megabook  Mythology: Timeless Tales of Gods and Heroes
Mythology: Timeless Tales of Gods and Heroes  Mậu Thân 1968 - Một Thiên Hùng Ca
Mậu Thân 1968 - Một Thiên Hùng Ca  Captain Underpants #5: Captain Underpants and the Wrath of the Wicked Wedgie Woman (Colour Edition)
Captain Underpants #5: Captain Underpants and the Wrath of the Wicked Wedgie Woman (Colour Edition)  Chinh Phục Không Gian - Hành Trình Kỳ Diệu
Chinh Phục Không Gian - Hành Trình Kỳ Diệu  Anna - Nếu một người trở về từ tương lai, cô ta sẽ làm xáo trộn thực tại của thế giới (Thái Hà)
Anna - Nếu một người trở về từ tương lai, cô ta sẽ làm xáo trộn thực tại của thế giới (Thái Hà)  Bốn Mùa, Trời Và Đất
Bốn Mùa, Trời Và Đất  3000 Tests Elementary To Intermediate (Không CD)
3000 Tests Elementary To Intermediate (Không CD)  ヴィンランド・サガ - Vinland Saga 23
ヴィンランド・サガ - Vinland Saga 23  Con Chuẩn Bị Vào Lớp 1 - Bé Tập Tô Các Nét Cơ Bản
Con Chuẩn Bị Vào Lớp 1 - Bé Tập Tô Các Nét Cơ Bản  Vở Tập Viết Có Mẫu Chữ - Quyển 2 _HA
Vở Tập Viết Có Mẫu Chữ - Quyển 2 _HA  Giáo Sư Đặng Hùng Võ & Những Người Bạn Nhà Báo
Giáo Sư Đặng Hùng Võ & Những Người Bạn Nhà Báo  Aquarium Snap
Aquarium Snap  Chứng minh của Wiles về Định lý cuối cùng của Fermat
Chứng minh của Wiles về Định lý cuối cùng của Fermat